ECDSA
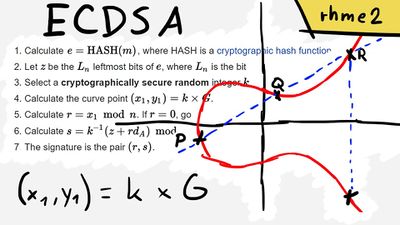
Elliptic Curve Digital Signature Algorithm (ECDSA) ist ein kryptographischer Algorithmus, der von Bitcoin verwendet wird, um sicherzustellen, dass das Geld nur von seinen rechtmäßigen Inhabern ausgegeben werden kann.
Inhaltsverzeichnis
Beschreibung
Vergleich der Schlüssel- und Signaturgröße zu DSA
Wie bei der Kryptographie mit elliptischen Kurven im Allgemeinen ist die Bitgröße des öffentlichen Schlüssels, von der angenommen wird, dass sie für ECDSA benötigt wird, etwa doppelt so groß wie die Sicherheitsstufe in Bit. Bei einer Sicherheitsstufe von 80 Bit (dh ein Angreifer benötigt zum Ermitteln des privaten Schlüssels maximal etwa 280 Vorgänge) würde die Größe eines öffentlichen ECDSA-Schlüssels beispielsweise 160 Bit betragen, während die Größe eines öffentlichen DSA-Schlüssels mindestens beträgt 1024 Bits. Andererseits ist die Signaturgröße sowohl für DSA als auch für ECDSA die gleiche: ungefähr 4 t Bits, wobei t das Sicherheitsniveau ist, gemessen in Bits, dh ungefähr 320 Bits für ein Sicherheitsniveau von 80 Bits.
Konzept
Einige Konzepte im Zusammenhang mit dem elliptischen Kurven-Algorithmus für digitale Signaturen:
- Privater Schlüssel: Eine geheime Nummer, die nur der Person bekannt ist, die sie erstellt hat. Ein privater Schlüssel ist im Wesentlichen eine zufällig generierte Nummer. In Bitcoin kann jemand mit dem privaten Schlüssel, der den Geldern des öffentlichen Kontos entspricht, das Geld ausgeben. In Bitcoin ist ein privater Schlüssel eine einzelne vorzeichenlose 256-Bit-Ganzzahl (32 Byte).
- Öffentlicher Schlüssel: Eine Nummer, die einem privaten Schlüssel entspricht, aber nicht geheim gehalten werden muss. Ein öffentlicher Schlüssel kann aus einem privaten Schlüssel berechnet werden, jedoch nicht umgekehrt. Ein öffentlicher Schlüssel kann verwendet werden, um zu bestimmen, ob eine Signatur echt ist (dh mit dem richtigen Schlüssel erzeugt wird), ohne dass der private Schlüssel preisgegeben werden muss. In Bitcoin werden öffentliche Schlüssel entweder komprimiert oder nicht komprimiert. Komprimierte öffentliche Schlüssel sind 33 Byte und bestehen aus einem Präfix (entweder 0x02 oder 0x03) und einer 256-Bit-Ganzzahl mit dem Namen x. Bei den älteren unkomprimierten Schlüsseln handelt es sich um 65 Byte, bestehend aus konstantem Präfix (0x04), gefolgt von zwei 256-Bit-Ganzzahlen, die als x und y bezeichnet werden (2 * 32 Byte). Das Präfix eines komprimierten Schlüssels ermöglicht es, den y-Wert vom x-Wert abzuleiten.
- Unterschrift: Eine Nummer, die belegt, dass eine Unterzeichnung stattgefunden hat. Eine Signatur wird mathematisch aus einem Hash eines zu signierenden Objekts plus einem privaten Schlüssel generiert. Die Signatur selbst besteht aus zwei Zahlen, die als r und s bezeichnet werden. Mit dem öffentlichen Schlüssel kann ein mathematischer Algorithmus für die Signatur verwendet werden, um zu bestimmen, dass er ursprünglich aus dem Hash und dem privaten Schlüssel erzeugt wurde, ohne den privaten Schlüssel zu kennen. Signaturen sind entweder 73, 72 oder 71 Byte lang, mit Wahrscheinlichkeiten von etwa 25%, 50% und 25%, obwohl Größen mit einer exponentiell abnehmenden Wahrscheinlichkeit sogar kleiner sind.
Sichetheit
Im Dezember 2010 gab eine Gruppe, die sich fail0verflow nannte, die Wiederherstellung des privaten ECDSA-Schlüssels bekannt, mit dem Sony die Software für die PlayStation 3-Spielkonsole signiert. Dieser Angriff funktionierte jedoch nur, weil Sony den Algorithmus nicht ordnungsgemäß implementierte, da k statisch statt zufällig war. Wie oben im Abschnitt „Algorithmus zur Signaturerstellung“ dargelegt, ist dA damit lösbar und der gesamte Algorithmus unbrauchbar.
Am 29. März 2011 veröffentlichten zwei Forscher ein IACR-Dokument, das zeigt, dass es möglich ist, einen privaten TLS-Schlüssel eines Servers mithilfe von OpenSSL abzurufen, der sich mit Elliptic Curves DSA über ein binäres Feld über einen Timing-Angriff authentifiziert. Die Schwachstelle wurde in OpenSSL 1.0.0e behoben.
Im August 2013 wurde bekannt, dass Fehler in einigen Implementierungen der Java-Klasse SecureRandom gelegentlich zu Kollisionen im k-Wert führten. Dies ermöglichte es Hackern, private Schlüssel wiederherzustellen, wodurch Bitcoin-Transaktionen genauso kontrolliert werden konnten wie die Besitzer legitimer Schlüssel, wobei derselbe Exploit verwendet wurde, mit dem der PS3-Signaturschlüssel bei einigen Android-App-Implementierungen verfügbar gemacht wurde, die Java verwenden und ECDSA zur Authentifizierung von Transaktionen verwenden .
Dieses Problem kann durch die deterministische Erzeugung von k verhindert werden, wie in RFC 6979 beschrieben.